The thermoelectric property optimizer combines the single-parabolic band model with diverse scattering mechanisms. Using empirical data, the optimized charge carrier concentrations can be determined. Furthermore, the temperature-dependent thermoelectric properties can be visualized and the total thermal conductivity can be separated into the electronic and lattice contributions. The second version includes the minimum thermal conductivity model and the Klemens model to determine the heat transfer of materials.
The software TOSSPB v2.0 can be downloaded here (as Executable) or to see the source code, please visit the GitHub respository (https://github.com/JanPohls/SPB-repo).
A graphical user interface (GUI) was developed to simply predict thermoelectric properties using empirical values. Calculate the Seebeck coefficient, Hall mobility, and Figure of Merit as function of carrier concentration.
Determine the thermoelectric figure of merit as function of carrier concentration and temperature. Three-dimensional plots can be exported and modified.
Compute and plot the electronic and lattice contribution to the thermal conductivity using different scattering mechanisms. This simple, fast approach can compare different scattering mechanism and the effect on the prediction of the lattice thermal conductivity.
Calculate the minimum thermal conductivity using diverse models (e.g., Cahill-Pohl, Pohls, Diffuse, Clarke). The temperature-dependent minimum thermal conductivity can be plotted to analyze low-temperature data.
Klemens model to predict how different doping elements on various sites will affect the lattice thermal conductivity (still in progress).
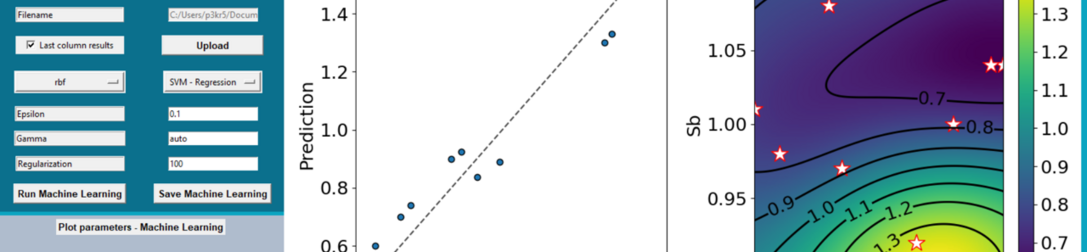
This software combines Design of Experiments with Machine Learning to accelerate the search of the optimized properties/reaction including optimizing to a desired value. A Latin Square approach was applied to study the entire phase space in a limited number of experiments. Up to 8 different variables can be simultaneously optimized to find the best outcome. The machine learning results can be visualized in all dimensions.
The software MODEM v0.4 can be downloaded here (as Executable) or to see the source code, please visit the GitHub repository (https://github.com/JanPohls/MODEM).
Design of Experiments to efficiently sample the entire phase space using a minimum number of experiments. All parameters (up to 8 parameters) can be tailored to the optimization process.
Graphical User Interface (GUI) to easily run machine learning optimizations and for the visualization of the results. This will increase the speed to find the optimum parameters for any problem.
Support vector machine regressions to interpolate the empirical data and visualize the phase space.
Carroll-Pöhls Lab
Last Update: November 14, 2024